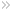The hydrogen 1S-3S transition
Similarly, to the 2S-4P experiment, the
purpose of measuring the 1S-3S transition freuquency in atomic hydrogen is to test the theory
of Quantum Electrodynamics (QED). Intuitively, one would say that such a test is conducted
by comparing theoretical predictions with experimental observations. Unfortunately, it is
not that simple. The theoretical expressions involve parameters that cannot be computed
from first principles and hence need to be determined experimentally. With n such parameters
one needs n measurements to get a hold of their values. Clearly, this does not test the
theory since the parameters can always be chosen to match theory and experiment. To test
a theory with parameters one needs to measure more independent quantities (here transition frequencies)
than there are parameters. When it comes to testing QED with hydrogen spectroscopy, we are left with 2
free parameters: the Rydberg constant Ry and the charge radius of the proton rp.
Further parameters, like the fine structure constant and the electron to proton mass ratio can
be determined more precisely from other experiments, that are more sensitive to those. In the spectrum
of atomic hydrogen, the 1S-2S transition frequency is measured most accurately by far, due to its very small
natural linewidth. Therefore, other measurements can be compared to each other, by calculating the
values of Ry and rp, they yield together with the 1S-2S measurement.
Checking the consitency of the parameters
Apart from hydrogen spectroscopy, the charge radius of the proton can also be measured by electron
scattering experiments or calculated, using quantum chromodynamics. Unfortunately, those methods do
not yet reach the required accuracy. The contribution of the size of the proton to our measurements
is truly tiny. However, since QED calculations of the hydrogen spectrum are among the most accurate
calculations physics has to offer, even a tiny contribution is important. In muonic hydrogen, where
the electron is replaced by its heavier brother the muon, this contribution much larger. Therefore
muonic hydrogen spectroscopy yields a much more accurate value for rp, even though
the measurement accuracy is much less. The figure summarizes the situation as of 2020.
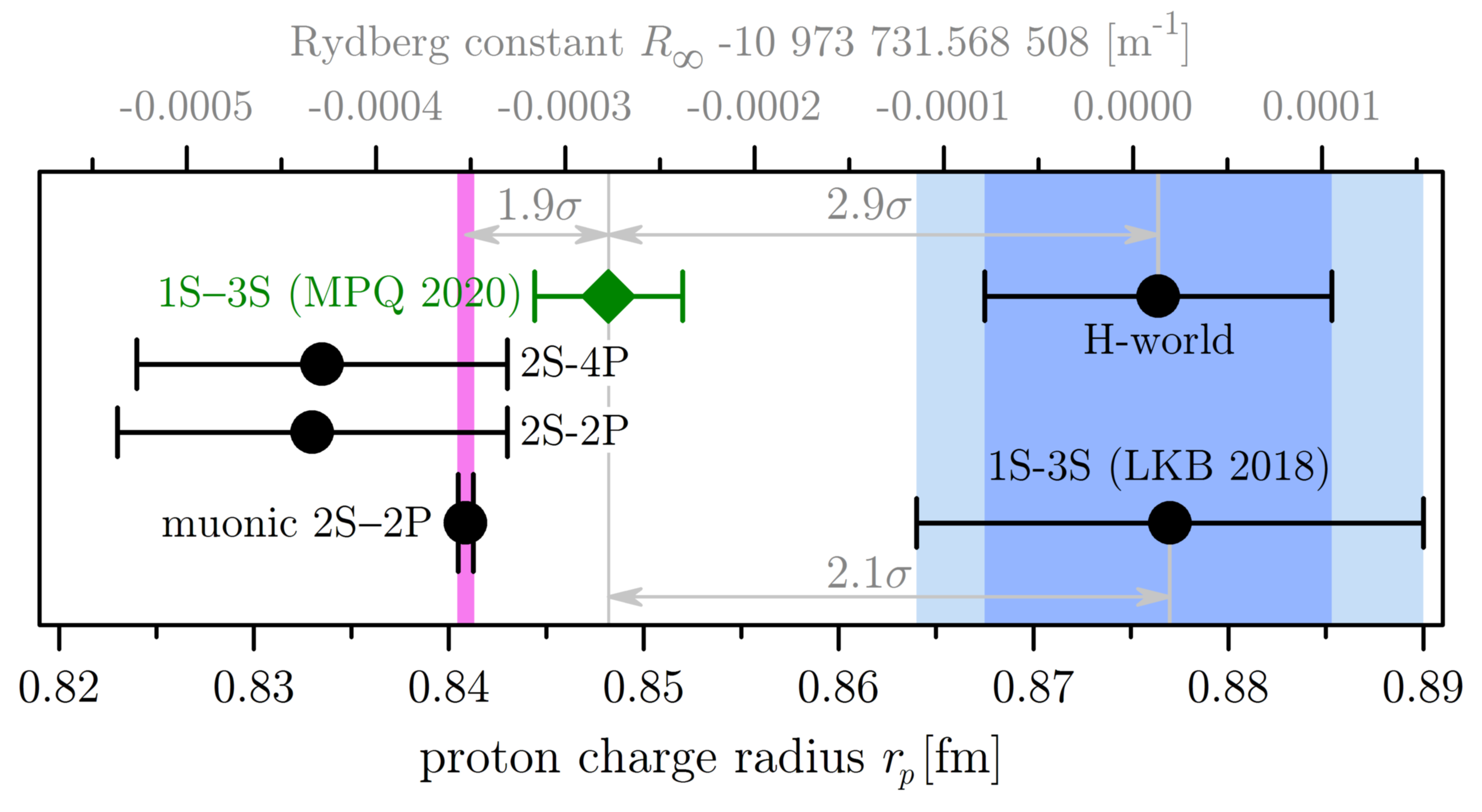
The proton charge radius measurements (bottom axis), as obtained from various experiments, partially disagree, preventing a verification of QED on the level of experimental uncertainties. Combining the 1S-2S and the 1S-3S (MPQ 2020) transition frequencies gives a significantly smaller value than the previous world data (H-world) obtained by using all hydrogen measurements (15 lines) available for the most recent published CODATA adjustment. In contrast, a continuous wave measurement of the 1S-3S transition frequency performed by our colleagues at the Laboratoire Kastler Brossel (LKB 2018) confirms the CODATA value. Our result is in reasonable agreement with our value derived from the 2S-4P measurement, with a radio frequency measurement of the 2S-2P transition, and with the value obtained from muonic hydrogen. Here we are not interested in the actual values of the parameters but in the consitency of the various values. The consitency check is the QED test.
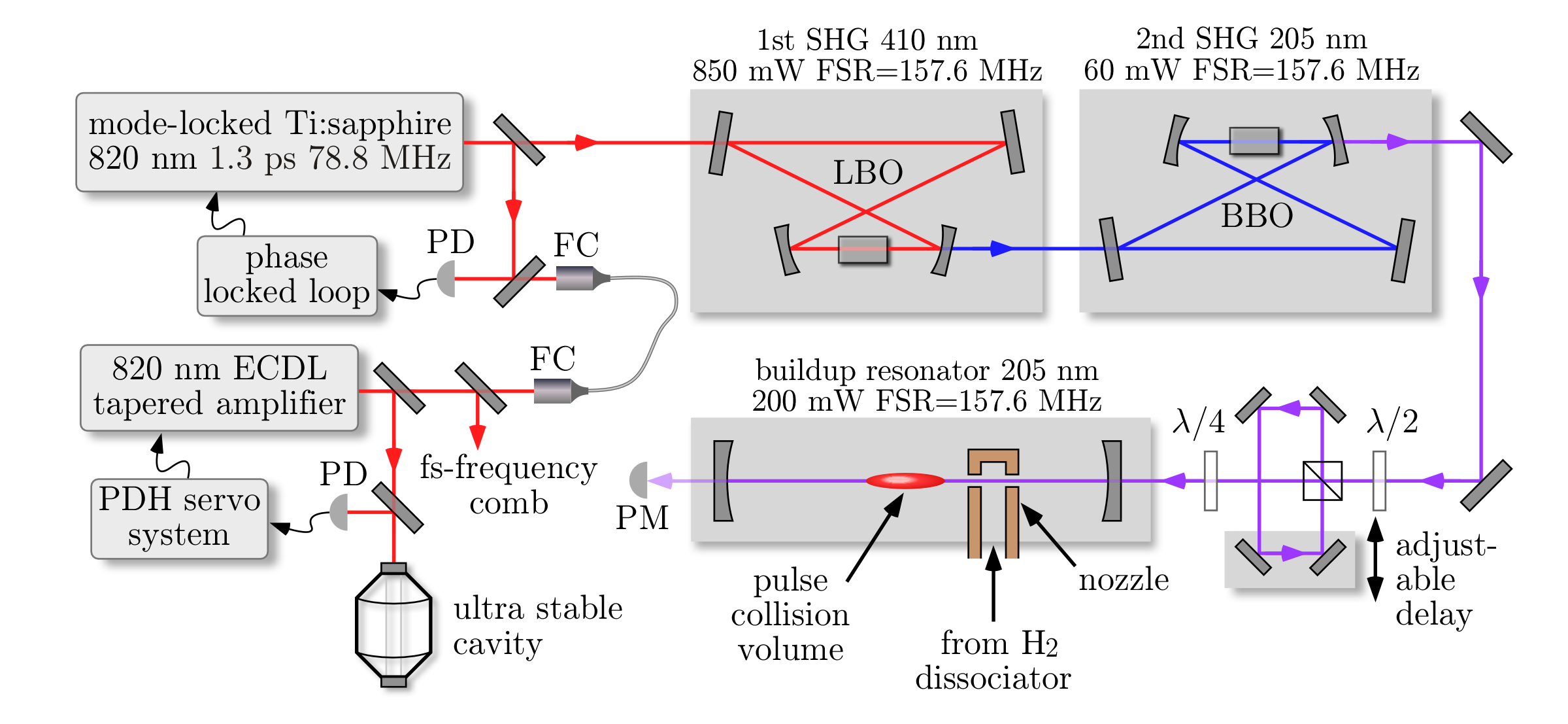
Experimental layout (PD = photo detector; P = photo multiplier; FC = fiber coupler; PDH = Pound-Drever-Hall)
Two-photon direct frequency comb spectroscopy
Similar to the 1S-2S experiment, we use
a cryogenic atomic beam and Doppler free two-photon spectroscopy with counter-propagating laser beams.
This laser is frequency doubled twice (SHG) to reach the transition wavelength of 205nm. In contrast to the
1S-2S experiment we use a pulsed mode locked laser rather than a continuous wave laser. With an adjustable
delay line we generate counter propagating pulse trains that meet at a small pulse collision volume
in the center of the 205nm buildup resonator. Doppler free excitation takes place only within this
volume. Pulsed excitation has several advantages adapted to the 1MHz linewidth without limiting the
observational linewidth due to time of flight broadening. It allows efficient collection of the signal
and limiting background light. More importantly, a small volume can be easily and homogenously shielded
against stray electric and magnetic fields. By varying the distance to the hydrogen nozzle collisional
shifts can be well characterized. Finally, the Doppler sensitive signal collected outside excitation volume,
that is very much independent of laser frequency, serves as a normalization signal to cancel fluctuations
of atomic flux and laser power. This feature significantly reduces the noise.
In the frequency domain the pulse trains are described by a regular spaced
frequency comb. Pairwise addition
of all comb modes provides an efficient excitation of the 1S-3S transition. It is important to note that the laser
linewidth that enters the line shape of the Doppler free signal, is given by the width of the individual
modes of the frequency comb rather than the inverse pulse duration. At the same time the frequency doubling
process is very efficient due to the increased peak power in a pulsed laser.
Current Members
Alexey Grinin, Derya Taray, Thomas Udem
Former Members
Arthur Matveev, Dylan Yost, Elisabeth Peters, Sascha Reinhardt
If you are considering joining our team as a Bachelor, Master or PhD student, or as a Postdoc, please email to: Thomas Udem
Further Reading
A. Grinin et al., Two-photon frequency comb spectroscopy of atomic hydrogen, Science 370, 1061 (2020)