Frequency Comb Project

Frequency combs to measure Cosmic Velocities

High resolution laser spectroscopy advanced a significant step forward when frequency combs were introduced to directly measure the frequency of the laser light that is used to excite atoms, ions or molecules. A prerequisite for this approach seems to be the coherence of the light source whose frequency is measured. On the other hand, there is a class of incoherent light sources that are scientifically interesting, but cannot be measured with coherent lasers. The most prominent of these light sources are astronomical objects like stars, galaxies and quasars. One of the possible exciting measurements is to determine the velocities of these objects from the Doppler shifts that their motion relative to the earth imposes on their spectra.

Spectrographs connected to telescopes have been used for that purpose, and they were typically calibrated against argon-thorium lamps or iodine absorption cells. The new generation of spectrographs, however, are limited in reproducibility by these calibration methods, because systematic shifts make it difficult to compare data recorded with different instruments. In addition, the lines of Th-Ar lamps are sparse so that non-linearities of the calibration curve of the spectrograph cannot be determined with high confidence. For this reason, we are now using a frequency comb that is directly stabilized to an atomic clock. The frequency comb possesses a dense grid of calibration lines that we can adjust to have a separation just above the resolution limit of the spectrograph.

The figure shows a section of the spectrum of the Sun around 189.3THz (1584nm). Visible in dark are Fraunhofer absorption lines of gaseous elements in the photosphere of the sun and as bright shorter vertical lines the calibration lines of the frequency comb.

Even though we just use a total of 58 lines from the comb and although the data was recorded with the Vacuum Tower Telescope at Tenerife, which is not designed for that purpose, we readily achieve a state-of-the-art calibration accuracy. We believe that using this technique with instruments specially designed by the European Southern Observatory (ESO) such as the High Accuracy Radial velocity Planet Searcher (HARPS) will reduce calibration uncertainties by 3 orders of magnitude.

Astronomers measure Doppler shifts as well as optical detunings in terms of the corresponding velocities. While the state of the art in instrument calibration is around 10m/sec (v/c=3e-8), we believe that 1cm/sec can be reached within the next years using frequency comb calibration. With this type of uncertainty, several intriguing observations will become possible. One of them is the detection of earth-like extra-solar planets orbiting sun-like stars from the recoil motion of the star. The required velocity resolution for the earth-sun system is 10cm/sec. In addition, when monitoring the cosmic red shift for a few years, it will be possible to decide whether the expansion of the universe is accelerating. This cosmic acceleration has been predicted from the pattern of the cosmic microwave background assuming the validity of general relativity. Such a direct observation could be decisive on whether or not dark energy, together with general relativity, constitute the proper model, or if we have to seek out for new explanations.

The main challenge of the frequency comb calibration method is to provide a mode spacing (i.e. repetition rate) that can be resolved by the spectrograph. The typical value at which astronomical telescopes achieve the best signal to noise ratio is around 10GHz. Our approach is to start out with a much lower mode spacing and use a Fabry-Perot etalon as a periodic filter to successively thin out modes.

If you want to read more about our work on astronomical frequency combs see:
Tilo Steinmetz et al. Science 321, 1335 (2008)

A press release with explanations for the non-physicist, graphs and animations
is found here in English and German

Frequency combs in the Extreme Ultraviolet (XUV)
by intracavity High Harmonic Generation (HHG)

Femtosecond laser optical frequency combs have revolutionized the measurement of optical frequencies and enabled optical atomic clocks. The same comb techniques are employed to control the carrier-envelope phase and thus the waveform of ultrafast laser pulses, which has led to the generation of single attosecond pulses. We hope that intracavity high harmonic generation (HHG) will open the door to another promising joint frontier of precision spectroscopy and ultrafast science. We are generating coherent radiation in the extreme ultraviolet (XUV) by high harmonic generation at the full oscillator repetition frequency of 10-100 MHz which is up to a 1000 times faster than previously possible with chirped pulse amplification or regenerative amplifiers. This high repetition rate causes the modes of the resulting XUV frequency comb to be well separated, allowing high resolution laser spectroscopy in this spectral region for the first time. Simultaneously, this method makes it possible to cover the full electromagnetic spectrum from infrared to soft X-rays with sharp and selectable continuous laser modes using the same set-up.

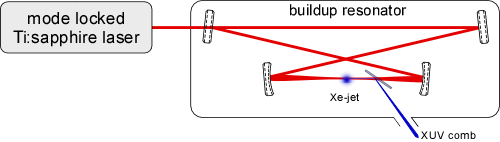We couple the pulses from a femtosecond Kerr-lense mode-locked laser into a high finesse optical resonator that contains a Xenon gas jet at the cavity focus as the nonlinear medium. Inside this resonator, the pulse energy is enhanced by a factor of 100 so that it can drive the nonlinear process (HHG). For cw lasers, enhancement factors exceeding 100,000 have been reached and overall nonlinear conversion efficiencies approaching unity can be achieved. In the case of a mode-locked ultrafast laser, however, complying with the following extra requirements is more difficult: The output spectrum of a mode-locked laser does not contain just a single cw mode but a comb of such modes. An optical resonator for such radiation has to be simultaneously resonant for each mode. This can be accomplished with a resonator of appropriate length and zero group velocity dispersion (GVD). As shown below, we have managed to extract microWatts of XUV power which should be sufficient to drive the 1S-2S transition in a hydrogen-like Helium ion with a reasonable rate (~1 Hz) provided that this power can be delivered and focussed onto the ion.

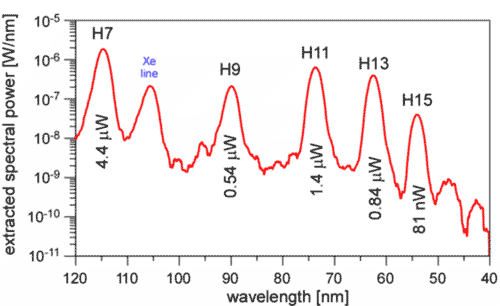While we were able to generate high harmonics with a mode spacing of 110MHz in 2005, the total generated power was far from being useful for high resolution spectroscopy, say, at the sharp 1S-2S transition in hydrogen-like He at 60.8nm. In the meantime, we have improved our system considerably and reduced the repetition rate to 10MHz. This mode spacing will still be sufficient to resolve individual modes with a sharp resonance, but allows for a 10 times higher pulse energy. Thanks to the highly non-linear character of HHG, this modified setup produced uW power levels for each harmonic as shown above. In principle this is sufficient to achieve a Hz type Rabi frequency for the 1S-2S transition in hydrogen-like He which is a typical value for a high precision single ion experiment. However, it remains to be shown whether we can actually deliver this power with a reasonable focus size to the ion.

If you want to read more about our work on intracavity high harmonics please see the following references:

Christoph Gohle et al. Nature 436, 234 (2005)
Akira Ozawa et al. PRL 100, 253901 (2008)

Welcome to the Frequency Comb project