Frequency
Combs
Frequency combs can be produced
by a pulse train of a mode locked laser. One can think of the comb
lines as the longitudinal cavity modes of that laser. Frequency combs
are simple and compact tools that phase coherently connect the radio
frequency domain (below say 100GHz) with the optical domain (above say
200THz). They greatly simplified high precision optical frequency
measurements and provide the long awaited clockwork mechanism for an
all-optical atomic clock. Optical precision spectroscopy is important
to determine fundamental constants like the Rydberg constant and test
the underlying theories. The most advanced of it, quantum
electrodynamics (QED), allows to calculate energy levels of simple
atoms such as the
hydrogen
atom with 12 digits of accuracy. With the frequency comb it is readily
possible to match this precision experimentally. Other spectroscopic
applications involve the search for possible slow temporal variations
of the fundamental constants that are suggested by some philosophical
arguments, tests of special relativity, and the precise calibration of
astronomical spectrographs to determine cosmic velocities (see below).
In the time domain, the frequency comb allows to stabilize the phase
between the carrier and the envelope of a pulse. This capability has
been a key element in the generation of attosecond pulses.


The pictures show the first self referenced frequency comb (left) in
1998 and the first octave spanning self referenced frequency comb
(right) in 1999 in our lab. Meanwhile fiber based laser systems have
taken over most practical applications.
To read more click here: pdf
Broadband Direct Frequency Comb Spectroscopy
There are several possibilities to employ the individual modes of a
frequency comb for massive parallel spectroscopy of, say, molecules
with their broadband spectra. For highest sensitivity, spectroscopy
should be conducted intra cavity to enhance the probing light
intensity. In that case one faces the problem of resonating all modes
at once. Another problem that arises is that the modes of most mode
locked lasers are too dense to be resolved with a common spectrometer.
Without resolving the comb lines, the frequency comb is nothing but a
broadband lamp in terms of resolution. With our Vernier type comb
spectroscopy, we solve both issues at once by using the enhancement
cavity also as a filter. If the mode spacing of the frequency comb and
the enhancement cavity that contains the sample are in a ratio that is
slightly off from an integer, individual modes can be readily selected
as sketched below.
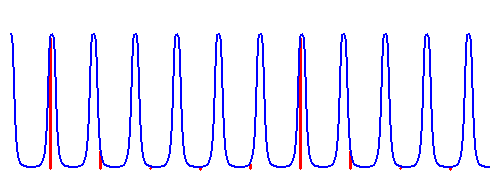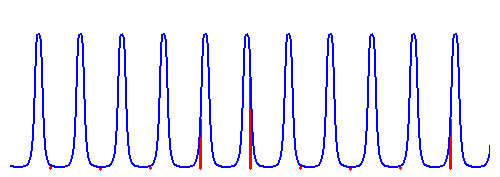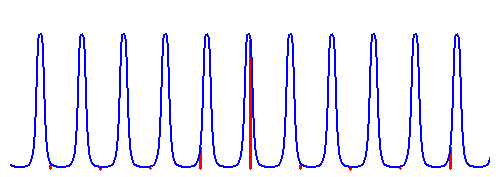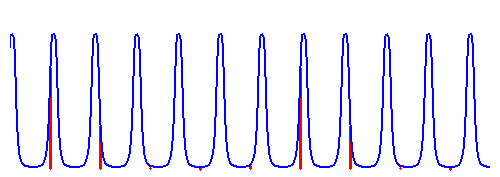
|
|
A
cavity with a spectral power enhancement expressed by an Airy
function (blue) is fed with a frequency comb (red). The mode
spacing of the comb and the cavities free spectral range are at a ratio of 5:6
such that only every 5th mode of the comb is resonant at a time. The
transmitted resonant modes are resolved by a small grating.
|
As an example, consider a 1GHz repetition rate laser coupled to a
cavity whose free spectral range is adjusted to around 0.99GHz.
In this case every 100th mode of the frequency comb (spaced by 100GHz)
is resonant, and those modes may be numbered as 0,100,200...
Scanning the comb slightly, modes with numbers 1,101,201... become
resonant and so on. By flipping a grating synchronized with this
scanning all modes of the frequency comb can be mapped on a CCD chip as
shown in the figure below.

|
|
Transmissions
through a cavity whose free spectral range is in close ratio of 1
with the mode spacing of the frequency comb coupled into the cavity.
Weak spots caused by absorption lines in the A bands of oxygen
are clearly observed.
|
The 2-dimensional array of spots on the CCD can be ordered uniquely
into a single frequency axis using a suitable computer program. Because
the spectroscopy cavity will not change the frequency of the
transmitted comb modes, each spot of the array can be readily traced to
an atomic clock. If necessary, the resolution of the method can be
increased beyond the repetition rate by repeating the measurement with
different positions of the frequency comb, thereby accessing components
that are narrow enough to fit in between the comb modes. The method is
sensitive to the dispersion of the sample while the dispersion of
the cavity does not change the frequency of the modes and therefore may
be subtracted out. When scanning over molecular resonances, one
observes the width of the cavity modes in frequency space. This
measurement is the equivalent to highly sensitive cavity ring down
measurement because the spectral width is given by the inverse ring
down time.
The method therefore:
- is providing the sensitivity of cavity ring down spectroscopy
- comes with an accuracy of the clock that controlles the
frequncy comb
- measures dispersion as well as absorption of the sample
- does not require a high resolution grating or spectrometer
- require cavity dispersion to be compensated for
If you want to read more about Vernier type
spectroscopy click here: pdf
Astronomical Frequency Combs
Frequency combs can also be useful to calibrate astronomical
spectrographs, significantly improving the calibration accuracy over
existing calibration methods. This has several fundamental
implications: Using periodically varying Doppler shifts of a distant
recoiling star, one can detect extraterrestrial planets in their
orbits. Also, by observing the variation of the cosmic red shift, it
would be possible to measure the dynamics of the Universe in real time.
This would allow to verify cosmological expansion without invoking
assumptions from an underlying model like General Relativity. Moreover,
measurements of gravitational red shifts on the surface of the sun
would benefit as well as the limits for a possible temporal variation
of the fine structure constant that could be improved by observing
distant quasars. In all of these examples, accuracies on the order of
parts in 1010 are required. As such an accuracy can be readily supplied
by a frequency comb, the challenge is to transfer it to astronomical
spectra. A prerequisite is that the modes can be resolved by the
spectrograph. This requires mode separations in the 10GHz range which
are difficult to reach for a fundamentally mode locked laser with the
required optical bandwidth of about one octave. Currently, our research
is aiming at achieving these goals in a system that can run
autonomously at a remote controlled telescope such as the Very Large
Telescope of the European Southern Observatory.

The picture shows a section of a solar
spectrum that we recorded at the Vacuum Tower Telescope at Tenerife
which is superimposed with a 15GHz frequency comb. The solar Fraunhofer lines
appear in dark while the comb lines are the shorter bright vertical lines.
To learn more about our recent work here.
XUV
Frequency Combs
We believe that XUV frequency
combs will enable high resolution laser spectroscopy at wavelengths
shorter than, say, 205nm which is about the shortest wavelength that
can be produced in nonlinear crystals (BBO) by second harmonic
generation. In order to be useful for this application the XUV
frequency comb must posses a mode spacing larger than the linewidth of
the investigated transition and posses enough power for a detectable
excitation rate. In the meantime we have experimentally met both of the
above requirements: The XUV frequency combs are produced from a fs mode
locked laser in the infrared (IR) by enhancing its pulse train in a
cavity that contains a Xe gas target for intracavity high harmonic
generation (HHG). The mode spacing in our apparatus is between 10 and
100MHz. By using the exciting pulse train as a frequency comb we can,
at the same time, determine the absolute frequency of each mode of the
XUV frequency comb. The traditional approach to produce XUV with pulsed
lasers (CPA + HHG) uses a repetition rate around 1kHz. Such a dense
frequency comb is basically useless for high resolution
spectroscopy, hence we would not even speak of a "comb" in that context.
|
|
|
The picture shows one of
our femtosecond enhancement cavities used to generate an XUV
frequency comb that has been loaded with an infrared pulse before
evacuation with dust particles.
|
Hydrogen
like Helium
The 1s-2s transition in hydrogen-like
helium is one of the most interesting candidates for high precision tests of
quantum electrodynamics (QED). Hydrogen-like 4He is an even simpler atom than
hydrogen as it shows no hyperfine structure. QED contributions to the energy
levels scale with the nuclear charge Z as Z4, thus providing a much more
sensitive probe than hydrogen. Even more interesting for theoreticians are
higher order contributions. The large uncertainty in the nuclear charge radius
of the proton is currently preventing meaningful comparisons between QED and
experimental data for hydrogen. Since the uncertainty of the charge radius of
the alpha particle is smaller than that of the proton, this problem is greatly
reduced for hydrogen-like helium. Last but not least, hydrogen-like He+ is
charged and can therefore be trapped and sympathetically laser cooled. We hope
to be able to excite the 60.8nm 1s-2s transition with our XUV frequency comb and
determine its absolute frequency.
|
|
|
The picture shows a linear radio frequency
ion trap that we are currently investigating to store magnesium ions that we
want to use for sympathetic cooling of helium ions.
|
Fiber Frequency Combs
Frequency combs based on Er and Yb doped
fiber mode locked lasers have very few adjustable parts and can therefore
operate autonomously for a very long time. This property is essential for
running an optical clock. In our group we operate two self-referenced fiber
laser combs that are referenced to a hydrogen maser and distributed to several
experiments throughout the institute. Besides re-locking them maybe once a
month or so, these combs need very little attention. The hydrogen maser is
continuously compared to the time signals broadcasted by the Global Positioning
System (GPS). Together with data from similar comparisons at the Physikalisch-
Technische Bundesanstalt (PTB) we can calibrate our frequency comb relative to
the cesium fountain clock there. Curently we are confident to perform this
calibration with a relative uncertainty of
10-14.
Optical Time Transfer
Long haul time transfer is currently done
within the radio frequency domain via GPS Common View or two-way satellite
links. With the frequency combs at hand, we can always transfer signals from
the optical to the radio frequency domain and back. Due to its much higher
frequency, two-way time transfer at the optical carrier should significantly
improve stability. For this project we acquired a 1000km fiber link connecting
the MPQ with the Physikalisch-Technische Bundesanstalt (PTB). We will transmit
a narrowband cw laser through this fiber to encode timing signals via the
optical carrier. The main challenge there is to compensate the fiber loss of
about 190dB and additional losses of optical components with optical
amplifiers, i.e. without converting to electronic signals, while maintaining
the round trip phase coherence.