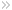Frequency combs
Frequency combs can be generated with a mode-locked laser that emits a
train of laser pulses. One can think of the comb lines as the longitudinal
cavity modes of that laser. Their frequencies are given by the boundary
condition that an integer multiple of wavelength has to fit into one cavity
round-trip. Frequency combs are simple and compact tools that phase coherently
connect the radio frequency domain (say below 100GHz) with the optical domain
(say above 200THz). They greatly simplified high precision optical frequency
measurements and provide the long awaited clockwork mechanism for an
all-optical atomic clock. Optical precision spectroscopy is important to
determine fundamental constants like the Rydberg constant and test the underlying
theories such as quantum electrodynamics.
Other spectroscopic applications involve the search for possible slow
temporal variations of the fundamental constants that are suggested by
some philosophical arguments, tests of special relativity, and the precise
calibration of astronomical spectrographs to precisely determine cosmic
velocities, for example to discover exoplanets.
In the time domain the train of short pulses from mode-locked laser is the
result of a phase coherent superposition of many continuous wave modes. The
stabilization of the comb allows to stabilize the phase between the carrier
and the envelope of a pulse. This capability has been a key element in the
generation of attosecond pulses.
As has been tested in many experiments, the modes are remarkably uniform, i.e. the separation between adjacent modes is constant across the frequency comb. This strictly regular arrangement is the most important feature used for optical frequency measurement and may be expressed as:
ωn = nωr + ω0
Here the mode number n of some 105 may be enumerated such that the frequency offset ω0 lies in the radio frequency domain. In doing so this number may be identified with the number of wavelength that fits into the cavity round-trip. By virtue of Fourier's theorem one can see that the mode spacing is the pulse repetition rate. With the help of this equation two radio frequencies ωr and ω0 are linked to the optical frequencies ωn of the mode-locked laser. The task is therefore to measure these radio frequencies.
Self-referencing
While the repetition frequency ωr of the mode-locked laser is easily
measured with a photodetector anywhere in the laser beam, it took a long time to set up
a good method to measure ω0. The established method is the so-called
self-referencing that becomes possible with an octave-spanning frequency comb. The
spectral width of a comb is roughly given by the inverse pulse duration, again by the
Fourier theorem. With a 10fs laser, that is readily available, the comb already covers
100THz which is not too far from the optical carrier frequencies. Therefore the spectral
width is not too far from an octave. Typically a full octave is obtained with further
spectral broadening by self-phase modulation. The offset frequency ω0
is then measured by doubling the frequencies of some modes at the "red" side of the comb
and beat them with modes at the "blue" side. A beat note is the frequency difference of
two optical frequencies. This is sketched below.
Self-referencing schematically
The idea of using optical frequency combs for metrology, i.e. precision measurements was born already in the 1970ies. However, the technology to produce octave-spanning combs became available in the 1990ies only. This idea turned out to be sufficiently important that it earned the 2005 Nobel Prize in physics.
Further Reading
Scott A. Diddams, Kerry Vahala and Thomas Udem, Optical frequency combs: Coherently uniting the electromagnetic Spectrum, Science 369, eaay3676 (2020)